
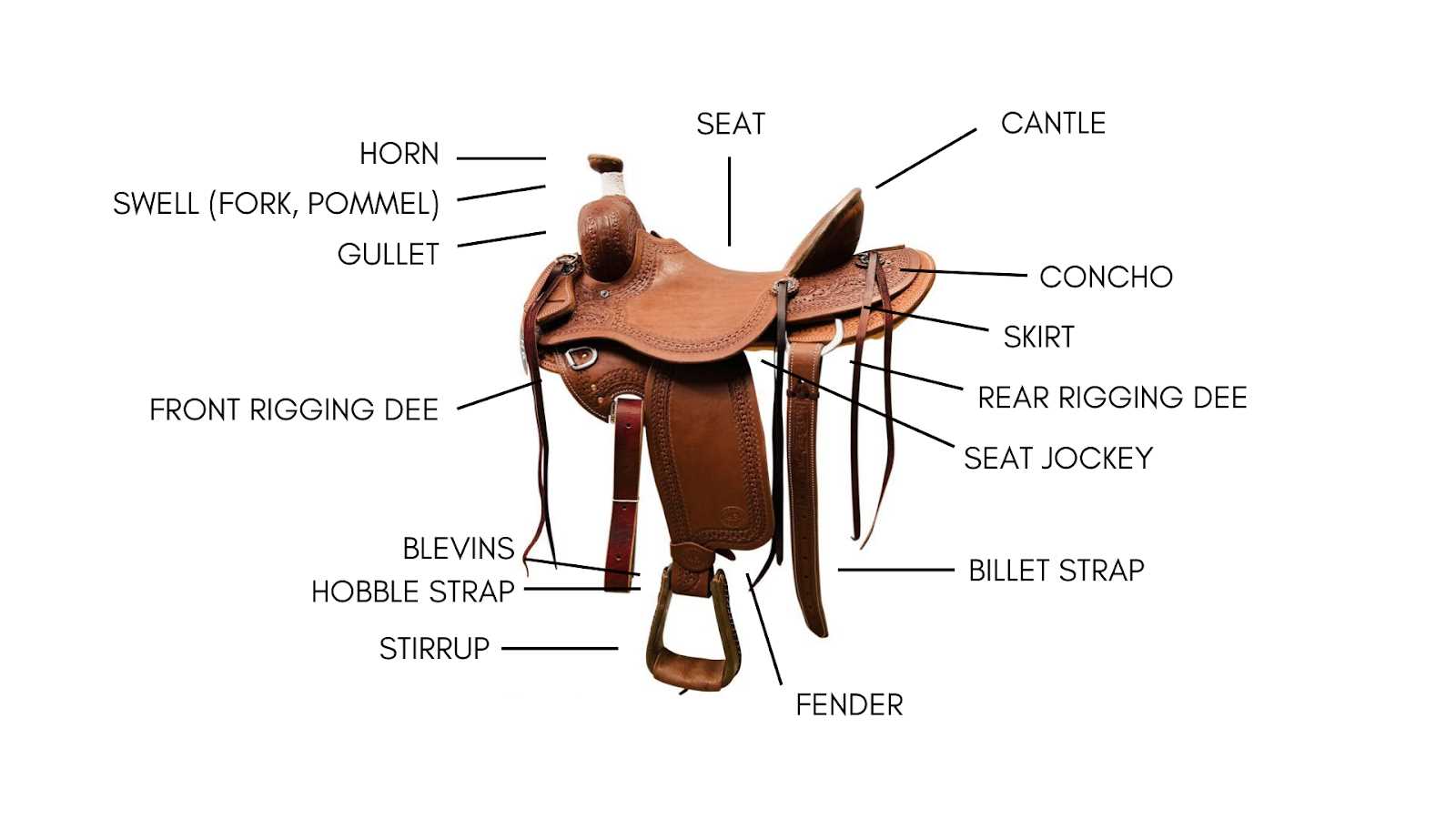
The essential structure of a riding apparatus plays a crucial role in both comfort and performance. Each element contributes to the overall function, ensuring a seamless connection between horse and rider. By exploring these elements, one can appreciate the intricate design that enhances the equestrian experience.
From the foundation that supports the weight to the elements that provide stability and control, every section serves a unique purpose. Understanding these components allows riders to make informed choices, optimizing their equipment for various disciplines and personal preferences.
Delving deeper into the anatomy of this equipment reveals how each aspect interacts with the others. The ultimate goal is to achieve harmony between rider and mount, fostering a bond that enhances both safety and enjoyment during riding adventures.
Understanding the Saddle Diagram

This section explores a graphical representation that reveals complex relationships in a multidimensional context. By examining this visual tool, one can gain insights into equilibrium points and the behavior of various functions across different variables.
Key Concepts
At the core of this representation lies the interaction between different axes, which allows for a clearer understanding of how changes in one dimension can affect outcomes in another. This interconnectedness is crucial for analyzing stability and optimization.
Applications and Benefits
Utilizing this model can enhance decision-making in various fields, from economics to engineering. By visualizing relationships, it becomes easier to identify optimal solutions and potential risks.
| Field | Application |
|---|---|
| Economics | Market equilibrium analysis |
| Engineering | Structural stability assessments |
| Data Science | Multivariable optimization |
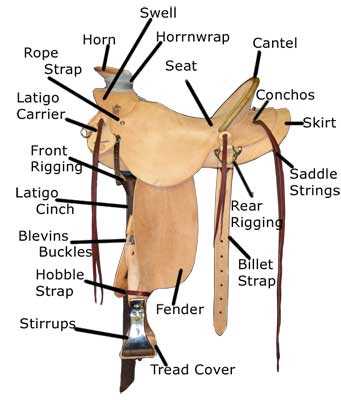
Key Components of Saddle Diagrams

The visual representation of complex systems often hinges on a few crucial elements that enhance understanding and analysis. These components serve as the foundation for interpreting interactions and relationships within a given context. Grasping their significance is essential for drawing insightful conclusions and facilitating further exploration.
Axes are fundamental in depicting the different dimensions of the analysis. They provide a reference framework, allowing for the comparison of various variables and their interplay. Typically, two axes are utilized, each representing a distinct variable, thus enabling a clear visual relationship.
Curves illustrate the behavior of the system under various conditions. These lines connect points that share similar characteristics, revealing trends and patterns. Understanding these curves is vital for identifying optimal solutions and potential challenges within the system.
Equilibrium Points denote specific states where forces are balanced. These points are critical for analyzing stability, as they indicate where the system can maintain its state without external influences. Recognizing these points aids in predicting the system’s response to changes.
Regions within the representation highlight areas of interest or significance. They can signify different operational conditions or outcomes, providing a visual cue for analysis. These zones are instrumental in categorizing responses and guiding decision-making processes.
Labels and Annotations enhance clarity by providing context to the visual elements. They guide the viewer’s understanding and ensure that the key features of the representation are easily interpreted. Well-placed labels can significantly improve the accessibility of complex information.
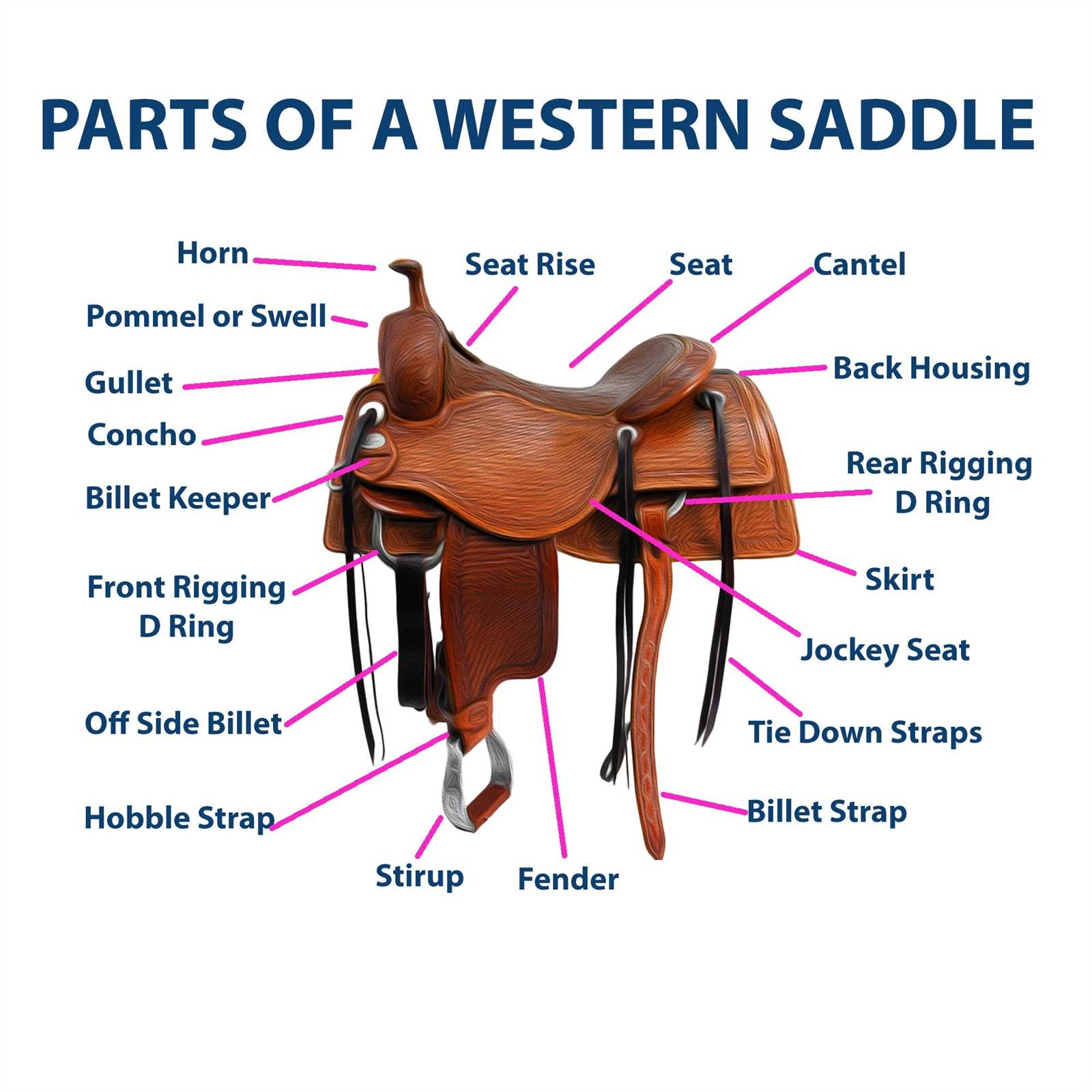
Types of Saddle Points Explained

Understanding various types of critical points in multi-dimensional spaces is essential for analyzing functions. Each type serves a unique role and presents different characteristics that influence the behavior of the function in its vicinity.
- Local Minima: Points where the function value is lower than that of nearby points.
- Local Maxima: Points where the function value is higher than that of surrounding points.
- Stationary Points: Points where the first derivative is zero, indicating a potential extremum.
- Hyperbolic Points: Points where the Hessian matrix has eigenvalues of opposite signs, leading to distinct curvature.
- Non-Hyperbolic Points: Points where the Hessian matrix has eigenvalues of the same sign, complicating the classification.
Each category plays a crucial role in understanding the structure and optimization of functions, making it vital to delve deeper into their properties and implications.
Applications in Optimization Problems

The analysis of critical points plays a significant role in various optimization challenges across multiple fields. By examining these points, researchers can identify local minima and maxima, guiding the search for optimal solutions. This approach is particularly valuable in mathematical modeling, machine learning, and economics, where decision-making relies on finding the best possible outcomes.
In machine learning, techniques that utilize these concepts enable algorithms to minimize loss functions, thus enhancing predictive accuracy. Gradient descent methods, for instance, leverage this analysis to iteratively approach optimal parameters.
In economics, understanding these critical points assists in resource allocation and maximizing utility functions, providing insights into market behavior and consumer preferences. This analysis ultimately leads to more efficient and effective strategies in both theoretical and applied scenarios.
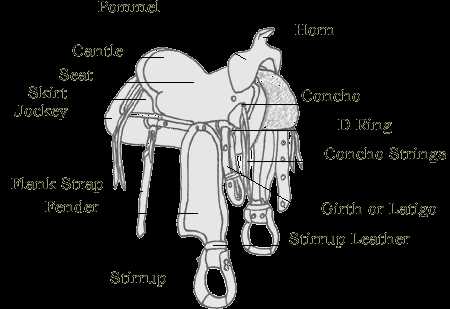
Visual Representation of Saddle Points
Understanding complex surfaces often requires a clear depiction of specific features that illustrate critical behavior. One such feature can be seen as a unique intersection where certain characteristics exhibit a balance between different directions. This section focuses on how these key points can be effectively illustrated through various visual methods.
There are several approaches to depict these distinctive locations:
- Graphical Plots: Utilizing 2D and 3D plots can help in visualizing the landscape around these points, showcasing how values change in proximity.
- Contour Maps: These provide a flattened view that indicates levels of function value, highlighting regions of interest where the behavior shifts.
- Surface Meshes: A three-dimensional mesh can enhance understanding by revealing the topography and allowing observers to perceive the structure from different angles.
Each of these methods serves to clarify the nature of these critical points, making them more accessible for analysis and interpretation. By examining how different representations convey the essential features, one can better appreciate their role in mathematical contexts.
Mathematical Significance in Analysis
Understanding the intricate relationships within multivariable functions reveals profound insights into their behavior. This exploration serves as a foundation for various applications across mathematics, economics, and engineering. Analyzing critical points allows researchers to discern stability and optimization in complex systems.
Critical Points and Their Implications
Identifying these key locations is essential for determining maxima, minima, and points of inflection. The nature of these points provides valuable information about the function’s overall structure, influencing decision-making and strategic planning.
Applications in Various Fields
The implications extend beyond pure mathematics; they play a crucial role in optimization problems, game theory, and even in machine learning algorithms. Grasping these concepts can lead to innovative solutions and enhanced understanding of dynamic systems.
Common Misconceptions About Saddle Diagrams
Understanding certain graphical representations can lead to confusion, especially when they are commonly referenced in various contexts. Many individuals hold misconceptions that can distort their interpretation and application of these visual tools.
- Oversimplification of Concepts: One prevalent misunderstanding is that these representations solely provide a straightforward view of complex systems. In reality, they often encapsulate multiple dimensions of information.
- Misinterpretation of Axes: Users frequently assume that the axes only indicate basic relationships. However, they often embody deeper mathematical or theoretical implications that require careful consideration.
- Uniformity in Shape: There is a belief that all such illustrations resemble a standard form. In fact, variations exist that are tailored to specific scenarios, each possessing unique characteristics.
By addressing these misconceptions, individuals can enhance their understanding and make more informed interpretations of these valuable visual tools.
How to Interpret Saddle Diagram Data
Understanding the information presented in a specific graphical representation involves recognizing key elements and their relationships. This approach allows for insightful analysis, enabling one to grasp the underlying trends and dynamics effectively.
Begin by identifying the axes: Each axis typically represents different variables, and their intersection indicates a crucial point of interest. Familiarize yourself with the scales to better comprehend the data distribution.
Next, observe the contours: These lines illustrate variations and help in visualizing areas of significance. Pay attention to peaks and troughs, as they often signify maximum and minimum values, respectively.
Finally, analyze the gradients: The slopes between points provide insights into the relationships and changes between variables. Steeper gradients may suggest stronger correlations, while flatter ones could indicate weaker connections.
By delving into these aspects, one can achieve a more comprehensive understanding of the graphical information and its implications.
Real-World Examples of Saddle Points
Understanding certain phenomena in various fields can be greatly enhanced by recognizing specific types of critical points. These unique positions often reveal interesting behavior and offer insights into complex systems. Below are a few illustrative scenarios where such points emerge in practical applications.
Economics: In market equilibrium analysis, the interaction of supply and demand curves can lead to critical points where neither buyers nor sellers have an incentive to change their behavior. These points help economists predict market stability and fluctuations.
Engineering: In structural analysis, critical points can identify load-bearing capacities. Engineers often use these concepts to ensure that structures can withstand varying forces without collapsing.
Biology: In evolutionary dynamics, certain strategies within populations can reach critical equilibria where different traits coexist. This balance can explain the persistence of diversity in ecosystems.
Physics: In optimization problems related to energy states, specific configurations can represent critical points. Understanding these configurations can help in the study of phase transitions and stability.